『脳はこうして学ぶ:学習の神経科学と教育の未来』スタニスラス・ドゥアンヌ

学習する動物というのは、過去の環境によって、今までとは異なる存在に変化することができ、したがって、その一生のあいだに、環境に適応できる動物のことである。
『サイバネティックス』ノーバート・ウイーナー

学習(learning)とは、世界に関する知識を得たことにより行動が変化することを意味する。
『カンデル神経科学』

学習とは何だろう。ラテン語の多くの言語では、学習(learning)のことを「つかむ(apprehending)」と語源が同じ言葉で表す。フランス語ではapprendreだし、スペイン語やポルトガル語ではaprenderとなる。実際、学習はばらばらの現実を把握し、それを捉え、自分の脳内に取り入れることだ。認知科学では、学習とは世界の内部モデルを形成することであるとする。私たちの五感を刺激する生データは、学習を通じて精製された概念となり、別の文脈でも再利用できる程度に抽象的になる－現実の縮尺何分の一かのスケール・モデルだ。
『脳はこうして学ぶ:学習の神経科学と教育の未来』スタニスラス・ドゥアンヌ

 

前著『意識と脳』では、著者の造語である「コンシャスアクセス」をキーワードとしながら「グローバル・ニューロナル・ワークスペース」という独自の意識の理論を展開したドゥアンヌ。今回は教育－学習－について正面から取り組み、本書を読み解くうえで重要な概念の一つである「ニューロン・リサイクル仮説」を打ち立てている。そんな本書の翻訳を担当されたのは、トマス・リッド『サイバネティクス全史』やロビン・ダンバー『ことばの起源』を訳されている松浦俊輔氏である。

 

スタニスラス・ドゥアンヌ(認知神経科学者でコレージュ・ド・フランス教授)。(右)は原著『How We Learn』(2021)

 

因みに「コンシャスアクセス」を一口に説明すれば、私たちは基本的に、特定の一時点をとりあげれば、一つの意識的な思考のみが可能にすぎない、というもの。もう少し具体的に述べれば、意識は能力が限られているため、新たな項目にアクセスするには、それまでとらえていた項目から撤退しなければならない。もっと注釈を加えれば、私たちには、いかなる瞬間にも、圧倒的な量の刺激が感覚器官に押し寄せているが、意識はそれらのごく一部にアクセスできるにすぎない。排除された不必要な情報は無意識の背景に留まったままでいる。

もう一つの「グローバル・ニューロナル・ワークスペース」の骨子は、「意識は脳全体の情報共有である」という単純なもの。脳は、それぞれが特定の機能に特化した、何十もの局所的なプロセッサーを備えている。評価システム(価値)、注意システム(注意の集中)、運動システム(未来)、知覚システム(現在)、長期記憶(過去)などである。コミュニケーションシステムたる「グローバル・ニューロナル・ワークスペース」は、それらのプロセッサー間での柔軟な情報の共有を可能にする。ワークスペースは、いついかなるときにも、いくつかのプロセッサーを選択してそれらがコード化する情報の一貫した表象を確立し、任意の期間心に保ち、他のほぼいかなるプロセッサーにも伝えられる。そして一片の情報は、ワークスペースにアクセスすれば必ずや意識される。上述で列挙した感覚入力および記憶からすべての必要な情報を集めて統合し、その結果を評価し、それについて好きなだけ時間をかけて熟考したうえで、実際の行動を導くというもの。

 

『意識と脳』(2015)と原著『Consciousness and the Brain』(2014)

 

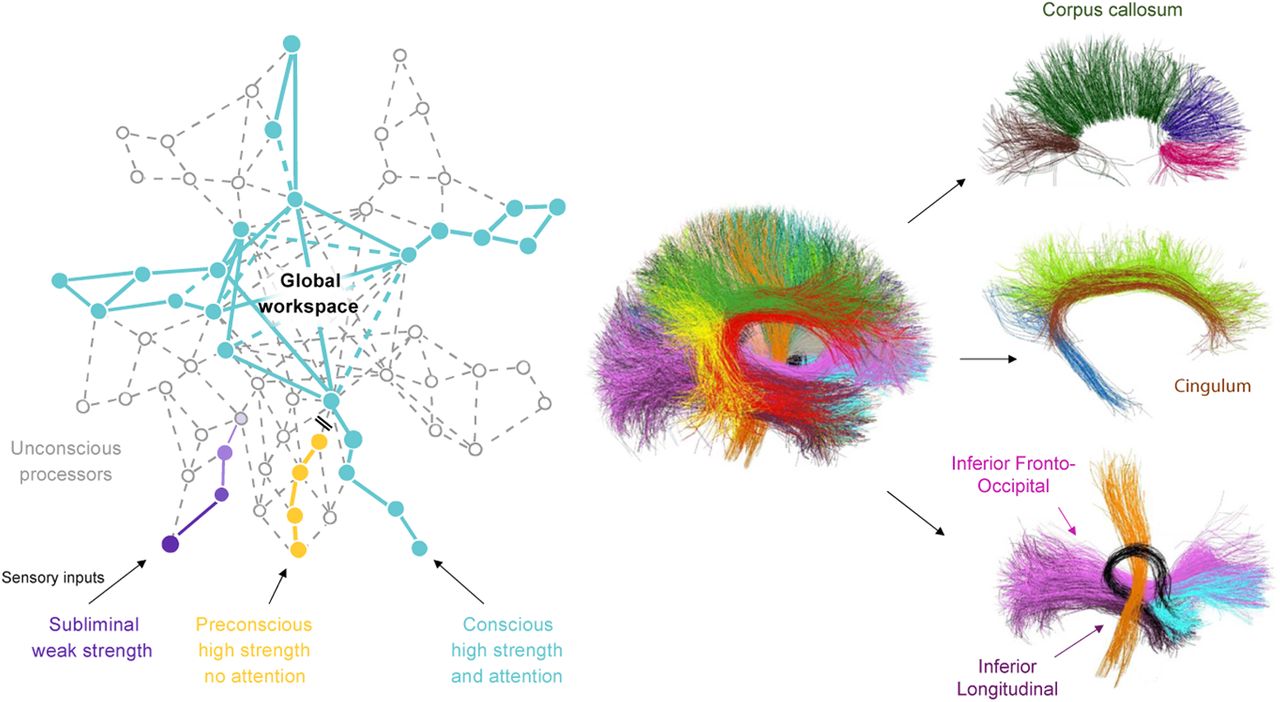
左がグローバル・ワークスペース

 

そして本書で展開されている「ニューロン・リサイクル仮説」とは、どのような仕組みなのか。ドゥアンヌの説明では、この仮説によれば、教育を受けるとは、既存の脳回路をリサイクルするということであり、何万年もの間、私たちは古いものから新しいものを作ることを学習してきた。学校で学習することはすべて、既存の神経回路を新たな方向に向け直すことであり、読んだり計算したりするために、子どもは既存の回路を転用する。そしてその回路はもともと別の用途のために進化したのだが、可塑性のおかげで新たな文化的機能に適応できるというものだ。ただし、その可塑性は無制約というわけではなく、空間的には数ミリの範囲に収まり、時間的には多くの回路が生後数カ月から数年で閉鎖され始めるという。

 

「脳は白紙だとする想定は明らかに間違っている。赤ちゃんは、核となる知識を相当に持った状態で、つまり自分がこれから遭遇する環境に関する普遍的な前提を豊かに備えて生まれる。その脳回路は誕生時にはよく組織されていて、赤ちゃんは、物体、人、時間、空間、数・・・・・と、あらゆる領域について強力な直観を備えている。赤ちゃんの統計学的技能は見事なものだ－みなすでに新米科学者なみにふるまい、高度な学習能力によって、徐々に、この世界に最もよく合うモデルに行き着くことになる」『脳はこうして学ぶ』スタニスラス・ドゥアンヌ

 

上述の指摘は、『数覚とは何か?』や『意識と脳』と同様に、ドゥアンヌの真骨頂である実証的知識を踏まえた上で導出されたものである。赤ちゃんが数や空間などの強力な直観を備えているというのは、『数覚とは何か?』で示されていたことである。この「ニューロン・リサイクル仮説」の核心的な一文に出会うまでには、脳の誕生から育ちの出る幕(ニューロンとシナプス、記憶の関係)などを順を追って説明されている。生まれ/育ちの論争も基調の一つであり、どちらの側も正しいということを示している。子供の読み方の学習は「ニューロン・リサイクル仮説」の一例で、私たちは読むために、元は視覚や話し言葉に充てられている脳のいくつかの領域を転用しているという。数に関しても巧みにリサイクルしており、私たちは生まれた時から、みな数を表象するための領域をもっていて、それを私たちは暗算にも使い、もっと高度な数学概念を考えている時のプロの数学者でさえ、脳の同じ領域を使っているという。

 

「パリの神経科学者スタニスラス・ドゥアンヌが書いているように、脳は新しいスキルと認知的・知覚的に関連があるスキルのためのニューロンネットワークをリサイクルし、再利用するのです。これは私たちの脳が限度内の可塑性の好例です」『デジタルで読む脳 X 紙の本で読む脳』メアリアン・ウルフ

 

「私がニューロン・リサイクル仮説を立てた意図は、通常の生態学的ニッチを超えるという人類の特異な才能を説明するためだった。人類は確かに、読んだり、書いたり、数えたり、計算したり、歌ったり、着飾ったり、馬に乗ったり、車を運転したりの新たな技能を獲得する能力がある点で独特なのだ。私たちの延長された脳可塑性は、新たな記号的学習アルゴリズムと組み合わさって、私たちに適応のための顕著な能力をもたらした－そして私たの社会は、子どもを日々学校という強力な体制に委ねることによって、自分たちの技能をさらに増幅する手段を発見した」 『脳はこうして学ぶ』スタニスラス・ドゥアンヌ

 

本書では、人工知能や学習アルゴリズムと比較をしながら学習の七つの定義を下し、「ニューロン・リサイクル仮説」を説明する。そして最後に学習の四本柱を掲げ、神経科学を踏まえた上での教育の重要性を指摘しながら、子供の潜在能力を最大限に発揮させるための一三か条を示して綴じられている。
 

 

長くなるので具体的には掘り下げられないが、ドゥアンヌの学習のおおまかな定義は、「学習するとは外的世界の内部モデルを形成する」ということであり、学習の四本柱とは、「注意」「能動的関与」「誤りフィードバック」「定着」という塩梅である。ドゥアンヌが列挙した「子供の潜在能力を最大限に発揮させるための一三か条」は、大まかにいえば、脳神経科医のオリヴァー・サックスが最後に手がけた『意識の川をゆく』での指摘に帰結できるだろうと個人的には感じている。
 

知性、想像力、才能、そして創造性は、知識とスキルの基盤がなければ何もならず、だからこそ教育は十分に体系化され、集中的でなくてはならない。しかし厳しすぎ、型にはまりすぎ、物語が少なすぎる教育は、活発で探求心旺盛な子どもの心を殺してしまうおそれがある。教育は体系と自由のバランスを取る必要があり、子ども一人ひとりのニーズは非常に変わりやすい。
『意識の川をゆく』オリヴァー・サックス
 

いわずもがな、本書は実証科学的に示されているので(それがドゥアンヌの真骨頂)、子どもの教育について、日頃から頭を抱えている学校の先生には特におすすめの一冊だ。ぼくは本書を読み通した後に、『意識と脳』を繙いた。そして再度、本書に手を伸ばした。ただ残念なのは、松浦さんの訳はぼくの好みではない、ということだ。他の方はどうなのかは理解しかねるが、トマス・リッド『サイバネティクス全史』を読んだ時と同様に頭に入り難い。
 

遊び、好奇心、社交、集中、睡眠についてのごく単純なアイデアで、私たちの脳の最大の技能である学習の力を増強することができるのだ。
『脳はこうして学ぶ』スタニスラス・ドゥアンヌ
 

人間は単に受け取った信号に受動的に反応しているだけではない。人間は自己の行為(活動)の計画やプログラムを形成し、行為の遂行を監視し、行動をそれらの計画やプログラムに適合させることで自己の行動を調節している。結局、人間は自己の行為の効果を本来の企図と比較し、自己が犯した誤りを訂正することで、自己の意識的活動を制御しているのである。
『ルリヤ　神経心理学の基礎　脳のはたらき』A.R.ルリヤ